https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 $-1$ 출력한다.
www.acmicpc.net
처음 이 문제를 볼 때는 2차 방정식을 생각했다.
조규현(이하 조)의 좌표와 백승환(이하 백)의 좌표가 주어지고 류재영(이하 류)까지의 각각의 거리가 주어지니까 가능하다 생각했다.
import sympy
n = int(input())
for i in range(n):
x1, y1, r1, x2, y2, r2 = map(int,input().split())
a,b = sympy.symbols("a b")
f1 = sympy.Eq((a-x1)**2+(b-y1)**2, r1**2)
f2 = sympy.Eq((a-x2)**2+(b-y2)**2, r2**2)
print(len(sympy.solve([f1,f2])))

나름대로 답이 나오긴 한다 ㅋㅋㅋㅋㅋ
하지만 백준에서는 sympy 모듈을 지원하지 않아서 ModuleNotFoundError가 발생했다.

다른 아이디어를 생각보니
조와 류까지의 거리로 가능하는 곳을 모두 찍어보면 하나의 원이 될 것이다.
그리고 백과 류까지의 거리로 가능한 곳을 찍어보면 또 다른 하나의 원이 될 것이다.
위 문제는 그 두개를 모두 만족하는 류의 좌표의 개수를 구하는 것이다.
그렇다면..?
가능한 경우는 조와 류까지의 원과 백과 류까지의 원의 접점의 개수를 의미한다
import math
n = int(input())
for i in range(n):
x1, y1, r1, x2, y2, r2 = map(int,input().split())
d = math.sqrt((x1-x2)**2 + (y1-y2)**2)
if d == 0: # 같은 동심원일 때
if r1 == r2: # 두 원이 같은 경우 (무한한 경우)
print(-1)
else: # 두 원이 다른 경우
print(0)
else: #원 중심이 다를 때
if d >= r1 and d >= r2: #한 원이 다른 원 밖에 있을 때
if d == r1+r2: # 두 원이 딱 붙을 경우 (접점이 하나)
print(1)
elif d > r1+r2: # 두 원이 서로 떨어져 있는 경우
print(0)
else: # 두 원이 겹쳐 접점이 두 개인 경우
print(2)
else: #한 원이 다른 원의 안에 있을 때
if d + r1 == r2 or d + r2 == r1: # 한 원이 다른 원 안에서 붙어 있는 경우
print(1)
elif d + r1 > r2 and d + r2 > r1: # 한 원이 다른 원 안에서 삐져 나올 경우
print(2)
else: # 한 원이 다른 원안에 들어가 있는 경우
print(0)
따라서 위의 아이디어로 이 문제를 해결할 수 있었다.
하지만 경우의 수를 생각하는 것이 어려웠다.
따라서 큰 경우 부터 조금씩 나눠서 생각했다.
1. 두 원이 같은 원인가? (동심원에 반지름까지 같을 때)
2. 한 원이 다른 원 안에 있는가? (각 경우마다 경우가 3가지 존재한다.)
1번은 문제에서 무한한 경우를 언급했기 때문에 금방 생각났다.
2번의 경우는 생각해내기 좀 어려웠다.
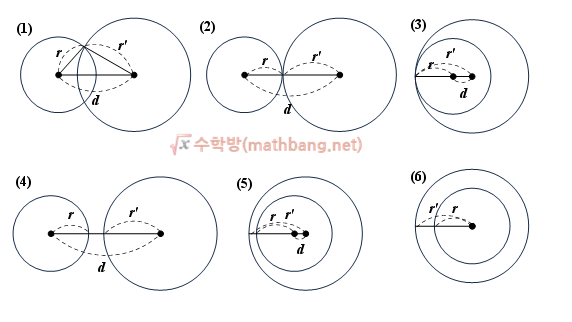
두 원이 만들수 있는 경우는
1. 멀리 떨어져서 접점이 없는 경우
2. 두 원의 거리가 반지름의 합과 같아 접점이 한개인 경우
3. 두 원이 겹쳐 접점이 두개인 경우
이다.
각각의 경우 0,1,2 개의 결과를 만들어낸다.
하지만 한 원의 중심이 다른 원 안에 있는지도 생각해야 한다.
따라서 총 6가지의 경우가 발생하게 된다.
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [백준] 2630번 : 색종이 만들기 (python 파이썬) (0) | 2024.04.18 |
|---|---|
| [백준] 15652번 : N과 M(4) (python 파이썬) (0) | 2024.04.18 |
| [백준] 1932번 : 정수 삼각형 (python 파이썬) (0) | 2023.01.24 |
| [백준] 2606번 :바이러스 (python 파이썬) (0) | 2022.12.31 |
| [백준] 1931번 : 회의실 배정 (python 파이썬) (0) | 2022.12.25 |