import sys
import heapq
t = int(input())
for _ in range(t):
n, k = map(int, sys.stdin.readline().split())
l = list(map(int, sys.stdin.readline().split()))
graph = [[] for _ in range(n)]
size = [0 for _ in range(n)]
# 위상 정렬을 위한 초기 설정
for _ in range(k):
start, end = map(int, sys.stdin.readline().split())
graph[start - 1].append(end - 1)
size[end - 1] += 1
w = int(input()) - 1
# 진입 차수가 0인 노드를 우선순위 큐에 추가
hq = []
for i in range(n):
if size[i] == 0:
heapq.heappush(hq, i)
# 초기 dp 설정
dp = l[:]
# 위상 정렬을 수행하며 dp 업데이트
while hq:
current = heapq.heappop(hq)
for next_node in graph[current]:
dp[next_node] = max(dp[next_node], dp[current] + l[next_node])
size[next_node] -= 1
if size[next_node] == 0:
heapq.heappush(hq, next_node)
print(dp[w])https://www.acmicpc.net/problem/1005
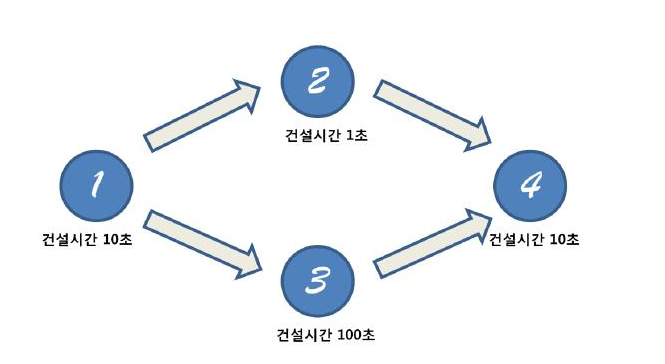

위 문제는 위상 정렬 + DP 를 이용해서 풀 수 있는 문제이다.
위 문제를 자세히 읽다 보면, 위상 정렬을 써야 해야 하는 것은 금방 생각해 낼 수 있다.
위 그림에서는 1번 노드부터 시작하지만, 1번 노드가 시작이 아닐 수도 있다.
위 문제에서 시작 노드는 진입 간선이 존재하지 않는 노드이다.
즉, 해당 노드가 목적지로 가는 길의 첫번 째 길이어야 한다.
진입 간선이 여러개일 수도 있다.
따라서 해당 문제는 위상 정렬을 사용해야 한다는 것을 알 수 있다.
두 번째로, 문제가 요구하는 조건은 무엇인지 생각해보자.
어느 건물로 가는 길이 여러가지 길이 있다면, 해당 길의 같은 진입차수의 건물이 모두 지어지고 나서야
다음 차수의 건물로 갈 수 있다.
이것은 무엇을 의미할까?
바로 최대 거리이다.
여러가지 출발지로 부터, 도착지까지 다양한 루트가 있을 것이다.
루트를 지나가기 위해서는, 해당 루트의 차수의 모든 건물이 지어져야 한다.
모든 건물이 지어지는 최소 시간은, 같은 차수의 건물 중 지어지는 최대 시간이다.
따라서, 위 문제는 위상 정렬을 수행하면서, 목적지 까지 가는 최대 시간을 DP 테이블에 업데이트 해나가는 문제이다.
따라서
1. 입력받는 간선의 정보를 이용해서 진입 차원을 계산하고,
2. 진입 차원이 0인 노드 (진입 간선이 없음 => 출발 지점)를 힙에 넣는다.
3. 힙에서 노드를 pop한다.
4. 해당 노드와 이어진 간선을 돌면서, dp 테이블에 최댓값을 업데이트 해나간다.
5. 간선과 이어진 다음 노드의 차원을 1 줄이고, 만약 해당 차원의 0이 되면(진입 간선이 없음) 힙에 넣는다.
6. 3~5번을 반복한다.
위 작업이 끝나면, dp 테이블에는, 해당 노드까지 가는 위상 정렬 경로의 최대 거리가 담겨있을 것이다.
정답을 출력하면 끝!
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [백준] 2580번 : 스도쿠 (python 파이썬) (0) | 2024.12.24 |
|---|---|
| [백준] 1197번 : 최소 스패닝 트리 (python 파이썬) (1) | 2024.12.14 |
| [백준] 1700번 : 멀티탭 스케줄링 (python 파이썬) + 벨라디의 변이 (2) | 2024.12.14 |
| [백준] 14719번 : 빗물 (python 파이썬) (1) | 2024.11.20 |
| [백준] 2504번 : 괄호의 값 (python 파이썬) (1) | 2024.11.19 |