https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net

맨 처음에는 2**n 크기의 2차 배열을 만든 후 순서대로 위치에 삽입하는 코드를 생각하고 작성하였다.
import sys
n,r,c = map(int, sys.stdin.readline().split(" "))
g = [[0 for i in range(2**(n-1))] for j in range(2**(n-1))]
x = 0
y = 0
num = 0
while True:
# x,y가 4/1 크기를 모두 돌면 탈출
if x >= 2**(n-1)-1 or y >= 2**(n-1)-1:
break
# z 모양으로 숫자 삽입
g[x][y] = num
g[x][y+1] = num+1
g[x+1][y] = num+2
g[x+1][y+1] = num+
# 숫자 및 x,y 좌표 바꾸기
num =num+4
x = x+1
y = y+1
# 특이점일 시 x,y 수정
if y+1 <= 2**(n-1)-2:
x = x-1
y = y+1
else:
x = x+1
y = 0
x = 2**(n-1)-1
y = 2**(n-1)-1
# 사분면 확인 후 계산
if x >= r and y>= c:
print(g[r][c])
elif x>= r and y< c:
print(g[r][c-2**(n-1)] + 2**(2*n-2))
elif x < r and y >= c:
print(g[r-2**(n-1)][c] + 2*2**(2*n-2))
else:
print(g[r-2**(n-1)][c-2**(n-1)] + 3*2**(2*n-2))하지만 N <= 15이기 때문에 위 방법은 N= 15일 경우 2**15 이상의 계산을 요구하기 때문에 시간초과 요류가 발생한다.
따라서 계산을 최소화하는 방향을 사용하며, N의 크기에 최대한 영향을 받지 않기 위해 N의 크기를 줄이는 아이디어를 떠올려야 한다.
N의 크기가 1 감소하면 2차원 배열의 크기는 기하급수로 줄어들기 때문에 이 방법을 반복하는 방법을 사용한다.
import sys
N, r, c = map(int, sys.stdin.readline().split(" "))
ans = 0
while N != 0:
N -= 1
# 1사분면인 경우
if r < 2 ** N and c < 2 ** N:
ans += ( 2 ** N ) * ( 2 ** N ) * 0
# 2사분면인 경우
elif r < 2 ** N and c >= 2 ** N:
ans += ( 2 ** N ) * ( 2 ** N ) * 1
c -= ( 2 ** N )
# 3사분면인 경우
elif r >= 2 ** N and c < 2 ** N:
ans += ( 2 ** N ) * ( 2 ** N ) * 2
r -= ( 2 ** N )
# 4사분면인 경우
else:
ans += ( 2 ** N ) * ( 2 ** N ) * 3
r -= ( 2 ** N )
c -= ( 2 ** N )
print(ans)

N = 3, r = 7, c = 7 일 경우의 예시를 생각해보자.
현재 n = 3 이며 (r,c)는 4사분면에 있다.

4 사분면에 있으므로 나머지의 개수는 2**(n-1) * 2**(n-1) * 3일 것이다. (2**(3-1) * 2**(3-1) * 3 = 48)
따라서 4 사분면에 시작하는 번호는 48이다.
이제 n에 1을 빼서 n = 2인 경우를 생각해보자. 이 경우에서는 N= 2 , r = 3, c = 3일 것이다. (N이 줄어들었으므로 r 과 c 또한 2**N만큼 줄어든다.
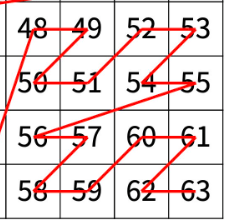
이 경우에도 (r,c)는 4 사분면이다. 따라서 나머지의 개수는 2**(n-1) * 2**(n-1) * 3 일 것이다. (2**1 * 2**1 * 3 = 12)
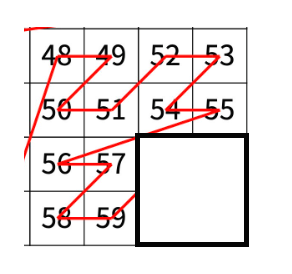
이제 또 n에서 1을 빼서 n = 1인 경우를 생각해보자. 이 경우에서는 N = 1 , r = 1, c = 1 일 것이다.
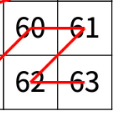
이 경우에도 (r,c)는 4분면이다. 따라서 나머지의 개수는 3일 것이다.
여기에서 N에서 1을 빼면 N= 0이 되버린다.
이제 지금까지 구했던 값을 모두 더해보자.
48 + 12 + 3 = 63 우리가 원했던 값이 나오게 된다.
따라서 가장 중요한 아이디어는
N의 값을 줄여가며, (r,c)가 몇 사분면인지 확인 한 후, 그 사분면 까지의 개수를 구하는 과정을 반복하는 것이다.
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [백준] 5430번 : AC (python 파이썬) (0) | 2022.06.04 |
|---|---|
| [백준] 1149번 : RGB거리 (python 파이썬) (0) | 2022.05.10 |
| [백준] 10026번 : 적록색약 (python 파이썬) (0) | 2022.04.16 |
| [백준] 1655번 : 가운데를 말해요 (python 파이썬) (0) | 2022.04.01 |
| [백준] 10844번 : 쉬운 계단 수 (python 파이썬) (0) | 2022.03.25 |